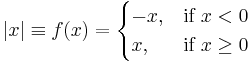Piecewise
In mathematics, a piecewise-defined function (also called a piecewise function) is a function whose definition changes depending on the value of the independent variable. Mathematically, a real-valued function f of a real variable x is a relationship whose definition is given differently on disjoint subsets of its domain (known as subdomains).
The word piecewise is also used to describe any property of a piecewise-defined function that holds for each piece but may not hold for the whole domain of the function. A function is piecewise differentiable or piecewise continuously differentiable if each piece is differentiable throughout its domain. In convex analysis, the notion of a derivative may be replaced by that of the subderivative for piecewise functions. Although the "pieces" in a piecewise definition need not be intervals, a function isn't called "piecewise linear" or "piecewise continuous" or "piecewise differentiable" unless the pieces are intervals.
Contents |
Notation and interpretation
Piecewise functions are defined using the common functional notation, where the body of the function is an array of functions and associated subdomains. For example, consider the piecewise definition of the absolute value function:
For all values of x less than zero, the first function (−x) is used, which negates the sign of the input value, making negative numbers positive. For all values of x greater than or equal to zero, the second function (x) is used, which evaluates trivially to the input value itself.
Consider the piecewise function f(x) evaluated at certain values of x:
| x | f(x) | Function used |
|---|---|---|
| −3 | 3 | −x |
| −0.1 | 0.1 | −x |
| 0 | 0 | x |
| 1/2 | 1/2 | x |
| 5 | 5 | x |
Thus, in order to evaluate a piecewise function at a given input value, the appropriate subdomain needs to be chosen in order to select the correct function and produce the correct output value.
Continuity
A piecewise function is continuous on a given interval if the following conditions are met:
- it is defined throughout that interval
- its constituent functions are continuous on that interval
- there is no discontinuity at each endpoint of the subdomains within that interval.
The pictured function, for example, is piecewise continuous throughout its subdomains, but is not continuous on the entire domain. The pictured function contains a jump discontinuity at 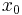 .
.